


The main catalog (Part II of this volume) is composed of 21 columns containing the following data:
All objects that are galaxies in the original Shapley-Ames Catalog are listed. They are shown in order of Right Ascension (1950). Since the best available positions are used, the sequence has occasionally been changed from the original SA.
Three SA objects have been omitted because they are not galaxies: NGC 643 is a cluster in SMC, NGC 2149 is a galactic, diffuse nebula, and NGC 6026 is a planetary nebula.
The identification of a few galaxies in the present catalog deserves comment.
NGC 1042: The Shapley-Ames galaxy NGC 1048 is a very faint spiral that clearly does not belong in the catalog. There is, however, a nearby bright spiral, NGC 1042, which should be included. We therefore assume that NGC 1048 in the original SA should read NGC 1042.
NGC 2646: It has been proposed (Seyfert, 1937; Hubble, private notes; RC1; RC2) that the Shapley-Ames galaxy NGC 2646 (BT = 12m.95) should be replaced by the Sa spiral IC 520 (mc = 12m.68). Although the latter galaxy is apparently somewhat brighter, actually both galaxies should have been included. We retain NGC 2646, whose position is correctly given in the original SA, and we list IC 520 in Appendix A among the known galaxies that should have been included by Shapley and Ames.
NGC 4183: The SA lists NGC 4160, but Seyfert's (1937) suspicion that this object is a star has been confirmed by de Vaucouleurs and de Vaucouleurs (RC1). Although the positions leave some discrepancy, the spiral galaxy referred to by Shapley and Ames can only be NGC 4183.
NGC 4342: The nomenclature of NGC 4342 has created considerable confusion in the past (Herzog, 1967). In spite of this, it is possible to relate all relevant observations (position, type, magnitude, velocity) unambiguously to this galaxy. To avoid future confusion, Herzog has proposed that the galaxy be exclusively referred to by its second designation, IC 3256. This has been followed by de Vaucouleurs et al. (RC2), but other recent authors still use the NGC designation (e.g., Nilson, 1973). For historical reasons we retain the designation NGC 4342 here.
NGC 4889: The Shapley-Ames galaxy listed as NGC 4872 is most likely NGC 4889 (Stebbins and Whitford, 1952), which is the brightest member of the Coma cluster.
IC 5179 = IC 5181: The Shapley-Ames galaxy IC 5186 is actually the galaxy IC 5179, which carries also the designation IC 5181 (RC2, p. 337; Corwin, 1977).
New 2: This galaxy is NGC 4507. 1 For historical reasons, we have maintained the designation New 2 of Shapley and Ames.
Two galaxies are designated HA85 (= Harvard Annals, Vol. 85) in the SA. To avoid conlusion, they are listed here as HA85-1 (= A 0509-14) and HA85-2 (= A 1852-45).
The present catalog contains 1246 entries.
These may prove useful for identification purposes, but completeness was not attempted. For the identification of Markarian objects (``Mark''), the Markarian lists I-X were consulted. We are greatly indebted to Dr. Mira P. Véron for a complete list of certain and probable radio sources (the latter are marked ``?''), which are identified with Shapley-Ames galaxies on the basis of the Catalog of Extragalactic Radio Source Identification (Véron and Véron, 1974; updated version, 1978). Two radio source identifications (with NCC 3689 and NGC 5444) given in the RC2 have not been confirmed.
The 1950 positions of the galaxies as given by Sandage (1978) or, where not given, from de Vaucouleurs et al. (RC2). For 46 southern galaxies, accurate positions were taken from Holmberg et al. (1974, 1975, 1977, 1978a, 1978b, 1979).
The decimals shown correspond to the accuracy with which the positions are known.
The Galactic Longitude and Galactic Latitude (1950) as given by de Vaucouleurs et al. (RC2).
The Supergalactic Longitude and Supergalactic Latitude (1950) as given by de Vaucouleurs et al. (RC2).
The classification was made by Sandage independently of previous determinations, but following the precepts set out elsewhere (Sandage, 1961, 1975a). The galaxies are classified in the sequence:
| - Sa Sb Sc Sd Sm Im | ||
| / | ||
| E0 - S0 - | ||
| \ | ||
| - SBa SBb SBc SBd IBm | ||
with intermediate classes (S0/a, etc.) and a new class, ``Amorphous,'' which replaces Irr (Sandage and Brucato, 1979). A few galaxies, mainly spirals, defy a definite classification. At this writing, some of the galaxies have inadequate plate material and may eventually be found to be normal or to have only minor peculiarities. As there are less than 20 such cases, at least 98 percent of the catalog galaxies can be fitted into the revised Hubble system.
Descriptive terms, such as ``pec'' (= peculiar), ``disrupted,'' ``tidal.'' ``ring'', ``jet'', and ``edge on,'' have been added in several cases. Barred spirals are designated as SB, intermediate types as S/SB.
The presence of an inner ring structure is indicated by (r) following the spiral subclass [e.g., SBab(r)]. Those spirals where the arms spring from the ends of the bar or are traced into the center are indicated by (s). Intermediate cases are designated with (rs). Where no information is given on the presence or absence of an inner ring, no decision could be made. Outer rings surrounding the galaxy are indicated by R preceding the type (e.g., RSa).
The E and S0 galaxies were classified according to their flattening, which, following Hubble, is defined as 10(a-b)/a. The subdivision of S0 galaxies into S01, S02, S03 according to the absence or the presence of dust is explained in Sandage (1961). Note that the subdivisions SB01, SB02, and SB03 in barred spirals refer to the character of the bar and not to the presence of dust, as explained in Sandage (1961).
The spiral and very-late-type galaxies are classified into luminosity classes as originally proposed by van den Bergh (1960a, 1960b, 1960c). The luminosity class of a spiral or Im galaxy is estimated from purely morphological features: the presence of spiral arms, surface brightness, and the degree of order (i.e., the coherence of the pattern and the arm thinness). The earliest class is called ``I,'' the latest class is ``V'' (not represented in the present catalog, but illustrated in the reproductions). Intermediate classes are given, either as half-class steps (e.g., III-IV) or in decimals (e.g., I.8), as explained by Dressler and Sandage (1978). Although the same symbols I-V are adopted as used by van den Bergh, the present classes cannot be assumed to correspond necessarily to his system. In particular, the calibration in absolute magnitude may not be the same. If a calibration of the present luminosity classes in absolute magnitude is attempted from the listed data, it should be remembered that the present catalog represents a magnitude-limited sample. The bias as a function of redshift in such a sample is of course severe (Sandage, Tammann, and Yahil, 1979) and must be accounted for (Tammann, Yahil, and Sandage, 1979).
The reliability of the classification depends on the angular size of the galaxy, the inclination in the case of spiral and Im galaxies, the quality of the available plate material, and strongly on the scale of the plate. A number of large-scale plates were used here for the first time; hence our classes may differ from those assigned by van den Bergh (1960c).
Our classification is rather conservative in the sense that the given types should be in error by not more than a subtype, and the luminosity classes in the mean by not more than half a luminosity class. The errors may be somewhat larger in those cases where small-scale plates had to be used or when the sky survey prints were the only source. Larger than average errors are indicated by ``:'' or ``?'' following the classification in cases where the galaxy may intrinsically defy a simple classification. In cases where the plate material is clearly insufficient, the types are given in parentheses () or brackets [].
Many galaxies were classified independently on plates from different telescopes. A comparison of the types shows that the use of plate material from different telescopes has not introduced systematic errors. The only exceptions are the prints of the Palomar Sky Survey, designated 48 Pr. The classifications from this source could be affected by some systematic errors, especially for galaxies of small angular size. Lower weight should be given to the corresponding types.
The galaxies of the present catalog are separately binned according to type in part III of this volume.
The following codes have been used:
| Number of | ||
| Code | Source | Galaxies |
| P200 | Palomar 200", glass plate | 304 |
| C100 | Las Campanas 100", glass plate | 491 |
| W100 | Mount Wilson 100", glass plate | 226 |
| W60 | Mount Wilson 60", glass plate | 160 |
| P48 | Palomar 48" -Schmidt, glass plate | 6 |
| 48 Pr | Palomar Sky Survey, paper print | 37 |
| C40 D | Las Campanas 40", glass plate | 12 |
| C40 IT | Las Campanas 40", image tube | 7 |
| UpS | Uppsala Schmidt, glass plate | 0 |
| W10 | Mount Wilson 10", glass plate | 2 |
| CTIO | 4m Cerro Tololo 4-meter | 1 |
| Total: 1246 | ||
A repetition of Column 1.
The magnitudes are given in the BT system of de Vaucouleurs et al. (RC2). The magnitudes come from the sources listed below and in Table 1:
(i) The RC2.
(ii) Many new source lists have become available that supersede the RC2. Examples are Sandage, 1975b; de Vaucouleurs, 1977; de Vaucouleurs and Corwin, 1977; de Vaucouleurs, Corwin, and Bollinger, 1977; de Vaucouleurs and Bollinger, 1977a, 1977b, 1978.
(iii) V26 and (b - V)0.5 values for E, S0, and a few early-type spiral galaxies, determined photoelectrically by Sandage and Visvanathan (1978), were transformed into the BT system. From galaxies with known (b - V)0.5 and (B - V)T, the relation
was established. The resulting B26 magnitudes were
compared with de
Vaucouleurs' BT for 291 galaxies in common. The
magnitude difference
does not depend on galaxy color (B - V), diameter
(D0), or flattening
(R25). There is, however, a type-dependent zero-point
difference:
Therefore the B26 magnitudes were corrected by
-0m.12, -0m.07, -0m.02, and
+0m.03 for E, E/S0, S0/E, and S0 galaxies, respectively. For the few
spiral galaxies with B26, a correction of +0.03 was
adopted. The
agreement between the corrected B26 and
BT magnitudes is very satisfactory, since the mean scatter is
For galaxies where the corrected B26 and
BT magnitudes are available,
a straight mean was adopted as the best value.
(iv) Multiaperture UBV measurements of southern galaxies (mainly
spirals) were kindly made available by
G. Wegner (1979)
before
publication. We have followed the precepts of the first approximation,
as given in the RC2 (e.g., equation 17a) to derive the logarithmic
aperture-diameter ratio
(v) Multiapertive UBV measurements for 39 galaxies from
Bucknell and Peach (1976)
and
Godwin et al. (1977)
have been reduced to BT
magnitudes the same way as the observations by Wegner (see source iv,
above). On the average, they are fainter by 0m.07 ±
0m.05 than the
weighted mean magnitudes from sources i-iv; this difference was judged
to be insignificant and was neglected. The random difference of the
magnitudes from source v and the mean from sources i-iv is
(vi) For a number of galaxies there are still no magnitudes determined
from detailed surface photometry or by photoelectric methods. For
these galaxies the magnitudes from the original Shapley-Ames catalog
were used, after reduction to the BT system. The
reduced magnitudes
were taken from the RC2, Column 15, upper line (see
de Vaucouleurs and Bollinger,
1977a).
(vii) For a few galaxies the original Shapley-Ames magnitudes could
not be transformed into the BT system. In these cases
the uncorrected,
original magnitudes have been used. The uncertainty of these
magnitudes is high (~ 0m.4).
No K-correction due to redshift has been applied.
A0 = 0m.132 (cosec b - 1) (for
|b| < 50°)
It should be remembered that the cosec law represents an idealized
case. The true Galactic absorption is very patchy and undoubtedly
depends on Galactic Longitude. Since the control of the absorption
dependence on position is judged to be insufficient for |b|
The internal absorption in E, S0, S0/a, and the earliest Sa galaxies
was assumed to be zero.
For later-type galaxies the internal absorption was calculated
following the principles of
Holmberg (1958),
who showed that the
internal absorption is proportional to cosec i (i = inclination).
Approximating cosec i by a/b (where a and b
are the major and minor
axes of the galaxy), Holmberg expressed the total internal absorption
Ai as
He determined the values of
This relation has the same form as the one derived by
Heidmann et al. (1972);
but these workers could not determine the value of
For the values of log a/b, we have used the values log
R25 as given in
the RC2 (Column 11). Our adopted values of
A special problem is posed by the Sa galaxies. Some of them appear
to be free of dust, whereas others clearly contain considerable
amounts of dust. This makes questionable whether the same internal
absorption correction can apply to all Sa galaxies and suggests that
Holmberg's high internal absorption corrections apply only to the
subsample of Sa galaxies with much dust. For this reason only Sa
galaxies with clearly visible dust have been corrected according to
the above precepts; for Sa galaxies without any traceable dust, zero
internal absorption was adopted, and for the intermediate Sa galaxies
only half the correction was applied. In the two latter cases the
value of Ai is marked with an asterisk (*).
The uncertainties of the internal absorption corrections are still
large. They may well contain systematic errors as large as ~
0m.5 for
highly inclined galaxies, and there may be systematic differences
between galaxies of different type due to errors in
There are several galaxies, including all those of class Amorphous,
for which no correction for internal absorption could be applied.
The magnitudes are calculated from the values given in columns 12, 13,
and 14.
The magnitudes are shown in brackets [ ] for those galaxies for which
no internal absorption correction could be applied.
The absolute magnitudes are calculated from the corrected apparent
magnitudes (Column 15) and the corrected velocities v0
(Column 20),
using an adopted Hubble constant of H0 = 50 km/s/Mpc
(Sandage and Tammann, 1976).
The procedure to derive distances to individual galaxies (and hence
absolute magnitudes) from the redshift (corrected to the centroid of
the Local Group) using a fixed value of H0 is
justified by the facts
that (1) the random radial velocities are typically
The only exceptions where v0 is not a reliable
distance indicator
are members of galaxian aggregates in which the velocity dispersion is
of the same order as the expansion velocity. The two most noteworthy
aggregates of this kind are the Local Group and the Virgo
Cluster. That they are exceptional in this respect is shown by the
fact that the only galaxies with negative v0 so far
known are members
of these two aggregates. Hence, for galaxies in the Local Group and in
the core of the Virgo Cluster (central 6° radius), and for a few
additional groups, we have adopted mean distances for the calculation
of absolute magnitudes. Table 2 lists those
clusters and groups
treated in this manner; the member galaxies are identified in the main
catalog by capital letters following the M value in Column 16.
A special problem is posed by the South Polar (or Sculptor) group. A
set of uniform plates taken of the late-type candidate members with
the Las Campanas 2.5-meter du Pont telescope shows pronounced
differences in resolution and hence in distance: NGC 300 is in the
foreground, NGC 7793 and probably NGC 253 lie in the background, while
NGC 55 and NGC 247 are between. Preliminary distances of these
galaxies are listed in Table 2. They are based on
the brightness of
the brightest blue and M supergiants in these galaxies
(Sandage, 1981).
The galaxies NGC 24 and NGC 45, which lie in the field of the
South Polar Group and at one time were considered to be members, are
definitely much more distant and lie, in agreement with their
redshift, at a distance of about 10 Mpc.
The greatest uncertainty in the group and cluster assignments in the
main catalog is for galaxies of the Virgo Cluster region (VR) between
6° and 10° away from the cluster center. Some of the galaxies in that
region may be foreground or background objects. However, in view of
the smaller velocity dispersion
[
The distance moduli are given in the preceding table for the two
cases where the Hyades modulus is 3.03 and 3.23. The latter value is
to be preferred (see
van Altena, 1974;
Hanson, 1980).
The mean errors of the listed absolute magnitudes for all field
galaxies in the catalog are compounded by the mean errors of the
apparent magnitudes (~ 0m.2), of the Galactic absorption
corrections (~ 0m.15), of the intrinsic absorption
corrections (~ 0m.25), and of the
corrected velocities (~ 50 km/s, corresponding to < 0m.1),
and by the
random deviations from an ideal Hubble flow (< 0m.1). Hence, the
compounded mean error in absolute magnitude is
Optical and 21-cm observations have been used. Only independent
determinations were considered: some authors have published the same
observations more than one time (occasionally with minor corrections).
In these cases we attempted to exclude all values except the latest.
The general agreement between optical and 21-cm redshifts and the
absence of any significant systematic difference is now well
established
(Roberts, 1972;
Rubin et al., 1976;
de Vaucouleurs et al.,
RC2;
Lewis, 1977;
Sandage, 1978).
The errors in redshifts quoted in
the original literature as determined from 21-cm observations are
quite consistent with independent 21-cm determinations. Hence, in most
cases the errors can be adopted as given in the original source.
However, the errors quoted by most optical observers are internal
errors. (An exception appears to be Humason's estimated errors of the
Mount Wilson velocities in
Humason et al., 1956.)
For the more
extensive lists of optical redshifts having sufficient overlap with
independent observations (especially 21-cm data), we determined the
true external mean errors. Typically these were found to be about
twice the quoted errors (see
Sandage, 1978).
A similar conclusion was
reached by de Vaucouleurs et al. (RC2, table 13), although the mean
errors they adopted for different observers are, in some cases, still
too small.
For small sets of redshift data where the overlap with independent
determinations is insufficient, the true external error was estimated
mainly from the spectroscopic dispersion used. The weighted mean
velocities were calculated using the adopted mean external errors.
Clearly deviating values were excluded.
No zero point corrections were applied to the velocities of any
source considered. Such zero point corrections may indeed by necessary
for some sources. For instance,
Roberts (1972)
has proposed that
optically determined redshifts with ~ 1200 < v < 2400 km/s are
systematically too large by ~ 100 km/s owing to blends of the galaxian
and night sky H and K lines, whereas
Lewis (1975)
has found this effect only in the Lick velocities from
Humason et al. (1956).
Different zero point corrections have also been applied by
de Vaucouleurs et al. (RC2, table 13). In our opinion, this complex
problem is not yet Settled. Even if one accepts certain zero point
corrections, they would be derived accurately only for spiral and
late-type galaxies where the precise 21-cm velocities exist. The
present 21-cm data for E and S0 galaxies are not sufficient to define
a mean correction for these types. In view of this situation and to
avoid a different treatment of galaxies of different type, we have
neglected any possible correction.
We have used 430 literature sources or private communications for
the velocities. These references contain 3437 velocity determinations
for galaxies in the present catalog.
More than five independent redshift determinations are available for
134 galaxies of the Catalog; from two to five determinations exist for
713 galaxies; and the velocity of 394 galaxies rests on only one
determination. No redshift data are known for one galaxy (NGC 3285).
The fact that velocity data are available for ~ 99 percent of the
catalog galaxies reflects the increasing number of redshift
determinations in the years since the end of the Humason-Mayall
program in 1956.
Several observers provided prepublication redshift data, as
acknowledged at the front of the volume and listed in References A.
The errors are compounded from the assigned errors of the
individual. velocity determinations, based generally on an estimate of
the external errors of the various observers (e.g.,
Sandage, 1978,
table XII). The mean errors of the catalog are distributed as:
The median error of the velocities is 40 km/s.
The values are calculated from solution number 2 of
Yahil, Tammann, and Sandage (1977):
The listed values
The true errors are generally the same as those of the uncorrected
velocities, except that in some directions the value of
Sources in parentheses have been rejected in the calculation of the
mean velocity and its mean error. The key for the references is given
in Relerences A at the rear of this volume.
1 The original catalog had New 2 = NGC
4517. Further investigation showed that the correct cross-identification
for New 2 is NGC 4507. (The
NED team).
Back.
 (
( B) = 0m.19 for E and E/S0, and
B) = 0m.19 for E and E/S0, and
 (
( B) = 0m16 for S0 and S0/E.
B) = 0m16 for S0 and S0/E.
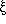 ,
which then leads from de Vaucouleurs
(1977,
table 1) to BT magnitudes. These magnitudes were not
originally
observed with an aim to derive total magnitudes; the measurements were
made with relatively small diaphragms. Therefore, a second
approximation to obtain BT is probably not
justified. A comparison of
these BT values with those of de Vaucouleurs (n
= 58) and those
derived from Sandage and Visvanathan (n = 50) gives a standard
deviation of
,
which then leads from de Vaucouleurs
(1977,
table 1) to BT magnitudes. These magnitudes were not
originally
observed with an aim to derive total magnitudes; the measurements were
made with relatively small diaphragms. Therefore, a second
approximation to obtain BT is probably not
justified. A comparison of
these BT values with those of de Vaucouleurs (n
= 58) and those
derived from Sandage and Visvanathan (n = 50) gives a standard
deviation of  =
0m.31 and 0m.27, respectively. This suggests the
standard deviation of a BT magnitude derived from Wegner's
observations to be
=
0m.31 and 0m.27, respectively. This suggests the
standard deviation of a BT magnitude derived from Wegner's
observations to be 
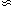 0m.25. The error
is smaller for galaxies observed with larger apertures
(
0m.25. The error
is smaller for galaxies observed with larger apertures
(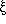
 -0.2), i.e.
-0.2), i.e.

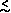 0.2, and somewhat
larger for cases where -0.2 >
0.2, and somewhat
larger for cases where -0.2 >
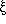 > -0.5. (No smaller aperture
measurements were considered.) Weight 1 was assigned to cases where
> -0.5. (No smaller aperture
measurements were considered.) Weight 1 was assigned to cases where
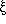
 -0.2 and weight 0.5 for smaller values of
-0.2 and weight 0.5 for smaller values of
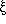 . The Harvard magnitudes
reduced to the BT system (as given in RC2, see
item 6) have standard deviations of ~ 0m.2
(de Vaucouleurs and Bollinger,
1977a);
they were
also assigned weight 1. BT values from de Vaucouleurs and his
collaborators and from Sandage and Visvanathan were assigned weight 2.
With these precepts, a total of 113 magnitudes from Wegner have been
incorporated into the catalog.
. The Harvard magnitudes
reduced to the BT system (as given in RC2, see
item 6) have standard deviations of ~ 0m.2
(de Vaucouleurs and Bollinger,
1977a);
they were
also assigned weight 1. BT values from de Vaucouleurs and his
collaborators and from Sandage and Visvanathan were assigned weight 2.
With these precepts, a total of 113 magnitudes from Wegner have been
incorporated into the catalog.
 =
0m.29. If the mean error of the latter is
=
0m.29. If the mean error of the latter is

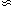 0m.15 to
0m.20, the magnitudes from source v have mean errors of
0m.15 to
0m.20, the magnitudes from source v have mean errors of
 = 0m.2 to
0m.25. We have
assigned errors between 0m.2 and 0m.3 to the
magnitudes from source v
according to the number of observations, the diaphragm size, and the
consistency of the individual measurements. Final magnitudes were
computed using the corresponding weights and the weights
of the magnitudes from sources i (from RC2), ii, iii, and iv.
= 0m.2 to
0m.25. We have
assigned errors between 0m.2 and 0m.3 to the
magnitudes from source v
according to the number of observations, the diaphragm size, and the
consistency of the individual measurements. Final magnitudes were
computed using the corresponding weights and the weights
of the magnitudes from sources i (from RC2), ii, iii, and iv.
Number of
Code* Source Galaxies
de Vaucouleurs and collaborators plus
Sandage(1975).
552
1) mean from de Vaucouleurs and collaborators and
from
Sandage and Visvanathan (1978)
245
2)
Sandage and Visvanathan (1978)
55
3) weighted mean from de Vaucouleurs and
collaborators and from
Wegner (1977)
27
4) weighted mean from
Sandage and Visvanathan (1978)
and from Wegner (1977)
27
5) weighted mean from Wegner (1977) and
corrected Harvard magnitude (RC2)
59
8) weighted mean from de Vaucouleurs and
collaborators and from
Bucknell and Peach (1976) or
Godwin et al. (1977)**
18
( ) Harvard magnitude reduced into the
BT system (RC2)
256
[ ] uncorrected Harvard magnitude as given
in the original Shapley-Ames catalog
7
* Refers to superscript entries in Column 12 of main
tabulation in Part II.
** There are also magnitudes availible from
Buckell and Peach (1976) or
Godwin et at. (1977)
for an additional 21 galaxies with superscript
1)-5).
A0 = 0m (for |b|
 50°).
50°).
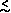 30°, no
attempt has been made to apply absorption corrections beyond the cosec
law. For some individual galaxies, particularly at lower latitudes,
this could well introduce errors of ~ 0.3 magnitude in the absorption
correction. The evidence for essentially absorption-free polar caps is
strong, however
(Sandage, 1973,
1975a;
Colomb, Poppel, and Heiles, 1977;
Burstein and Heiles, 1978),
and use of the adopted absorptions
for |b|
30°, no
attempt has been made to apply absorption corrections beyond the cosec
law. For some individual galaxies, particularly at lower latitudes,
this could well introduce errors of ~ 0.3 magnitude in the absorption
correction. The evidence for essentially absorption-free polar caps is
strong, however
(Sandage, 1973,
1975a;
Colomb, Poppel, and Heiles, 1977;
Burstein and Heiles, 1978),
and use of the adopted absorptions
for |b| 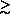 30°
should give negligible systematic errors.
30°
should give negligible systematic errors.
 X a/b.
X a/b.
 and the maximum values of Ai for edge-on
galaxies of different spiral types. However, there are now indications
that his maximum values are too large (see
Sandage and Tammann, 1976).
Therefore, the maximum values have been tentatively reduced here to
the upper limits given below. We have adopted interpolated values so
as to obtain a smooth transition between the absorption values from
the cosec law at small inclinations and the maximum absorption at high
inclination (a/b
and the maximum values of Ai for edge-on
galaxies of different spiral types. However, there are now indications
that his maximum values are too large (see
Sandage and Tammann, 1976).
Therefore, the maximum values have been tentatively reduced here to
the upper limits given below. We have adopted interpolated values so
as to obtain a smooth transition between the absorption values from
the cosec law at small inclinations and the maximum absorption at high
inclination (a/b  4.7). Our
empirical absorption law can be well represented up to
Aimax by
4.7). Our
empirical absorption law can be well represented up to
Aimax by
 +
+
 log a/b.
log a/b.
 (the
absorption correction of a face-on spiral), and they found,
surprisingly, that
(the
absorption correction of a face-on spiral), and they found,
surprisingly, that  is constant for galaxies of type Sa to Im.
Instead, we have adopted the numerical values of
is constant for galaxies of type Sa to Im.
Instead, we have adopted the numerical values of
 for different types
of galaxies as given by
Holmberg (1958). The
for different types
of galaxies as given by
Holmberg (1958). The
 -value for Im galaxies
was chosen to give a mean internal absorption correction of ~
0m.3, as suggested by
Holmberg (1964).
-value for Im galaxies
was chosen to give a mean internal absorption correction of ~
0m.3, as suggested by
Holmberg (1964).
 ,
,  , and Aimax are:
, and Aimax are:
Galaxy Type 

Aimax
Sa, Sab, Sb 0m.43 1m.34
1m.33
Sbc, Sc, Scd, Sd 0m.28 0m.88
0m.87
Sdm, Sm, Im 0m.14. 0m.44
0m.43
 and
and
 . In
addition, nothing is known about the scatter of individual galaxies
about the mean relation. However, we believe that, in general, the
internal-absorption-corrected magnitudes are closer to the true
luminosity than are the uncorrected magnitudes, because it is clear
that some correction is necessary. The mean value of
Ai is ~ 0m.5 for
spirals and lm galaxies taken as a whole. Clearly then, the mean error
of Ai is less than ~ 0m.3.
. In
addition, nothing is known about the scatter of individual galaxies
about the mean relation. However, we believe that, in general, the
internal-absorption-corrected magnitudes are closer to the true
luminosity than are the uncorrected magnitudes, because it is clear
that some correction is necessary. The mean value of
Ai is ~ 0m.5 for
spirals and lm galaxies taken as a whole. Clearly then, the mean error
of Ai is less than ~ 0m.3.
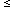 50 km/s/Mpc
(Sandage and Tammann, 1975;
Fisher and Tully, 1975;
Tammann et at., 1980),
and (2) H (local)
50 km/s/Mpc
(Sandage and Tammann, 1975;
Fisher and Tully, 1975;
Tammann et at., 1980),
and (2) H (local)
 H0 (global)
(Sandage, Tammann, and Hardy, 1972;
Tammann, Yahil, and Sandage, 1981).
Even for a field galaxy like
NGC 3109 with an exceptionally small radial velocity of
v0 = 129 km
s-1 the error in the distance introduced by the random component of
the radial velocity is
H0 (global)
(Sandage, Tammann, and Hardy, 1972;
Tammann, Yahil, and Sandage, 1981).
Even for a field galaxy like
NGC 3109 with an exceptionally small radial velocity of
v0 = 129 km
s-1 the error in the distance introduced by the random component of
the radial velocity is 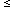 40 percent,
corresponding to an error of only
40 percent,
corresponding to an error of only
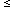 0m.8 in M. For galaxies
with v0 > 500 km/s, a random motion of 50 km
s-1 will cause an error in M of only < 0m.2.
0m.8 in M. For galaxies
with v0 > 500 km/s, a random motion of 50 km
s-1 will cause an error in M of only < 0m.2.
 (v) = 445 km
s-1] of the external
region compared with the central cluster core where
[
(v) = 445 km
s-1] of the external
region compared with the central cluster core where
[ (v) = 690 km/s,
and considering that the mean velocities of the central core and the
outer region are the same to within the errors, most galaxies of the
outer region must lie at the same mean distance as the cluster proper.
(v) = 690 km/s,
and considering that the mean velocities of the central core and the
outer region are the same to within the errors, most galaxies of the
outer region must lie at the same mean distance as the cluster proper.
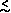 0m.4.
0m.4.
Group or Cluster
Designation <v0>
Nr. of SA galaxies
(m-M)° a
(m-M)° b
Source c
Local Group L 10
M31 24.12 24.32 1
NGC 147 24.12 24.32 1
NGC 185 24.12 24.32 1
NGC 205 24.12 24.32 1
NGC 221 24.12 24.32 1
LMC 18.59 18.79 1
SMC 19.27 19.47 1
M33 24.56 24.76 2
NGC 6822 23.95 24.15 2
IC 5152 (26.0)
South Polar Group S 5
NGC 300 26.7 26.9 3,4,9
NGC 55 27.3 27.5 4
NGC 247 27.3 27.5 4
NGC 7793 27.9 28.1 4
NGC 253 27.9 28.1 4
M81 / NGC 2403 Group N 240±22 7 27.56
27.76 5,6
NGC 5128 Group C 255±25 6
29.0
29.2 7
M101 Group M 368±23 4
29.2 29.4
8,6,7
Virgo Cluster
(a) within 6° V 1026±75 85 31.5
31.7 6
(b) between 6° and
10° from center
VR 1147±93 23 31.5 31.7 6
Fornax Cluster F 1486±76 19
32.4
from<v0>
a (m - M)°
corresponding to (m - M) Hyades = 3.03.
b (m - M)°
corresponding to (m - M) Hyades = 3.23.
c Sources: 1.
Sandage and Tammann, 1971;
2. Sandage and Tammann, 1974a;
3. Graham, 1979;
4. Sandage, 1981;
5. Tammann and Sandage, 1968; 6.
Sandage and Tammann, 1976;
7. Tammann, 1977;
8. Sandage and Tammann, 1974b;
9. Melnick, 1978.
 , km/s
, km/s n
 , km/s
, km/s n
< 10 239 100-149 80
10-24 251 150-199 24
25-49 293 200-249 17
50-99 338 250-300 3
 v to be applied to the observed
velocity to obtain the velocity relative to the centroid of the Local
Group
v to be applied to the observed
velocity to obtain the velocity relative to the centroid of the Local
Group
 v = -79 cos l cos
b + 296 sin l cos b - 36 sin b.
v = -79 cos l cos
b + 296 sin l cos b - 36 sin b.
 v
differ from this formula by up to ± 3 km/s
because they were computed with a formula in which the coefficients
were not rounded off.
v
differ from this formula by up to ± 3 km/s
because they were computed with a formula in which the coefficients
were not rounded off.
 v relative to
the centroid of the Local Group
v relative to
the centroid of the Local Group
 v depends
strongly on the exact form of the adopted correction formula. In these
cases, the remaining uncertainry due to uncertainties in the adopted
apex and velocity of the Yahil et al. solution may introduce
additional systematic errors of ~ 60 km/s.
v depends
strongly on the exact form of the adopted correction formula. In these
cases, the remaining uncertainry due to uncertainties in the adopted
apex and velocity of the Yahil et al. solution may introduce
additional systematic errors of ~ 60 km/s.